Performance Benchmarking on
Queries of a New Category with Variations in
Indexing and Object Database Sizes
Performance Comparison with Multiple Query Conditions in an Object Hierarchy
There is a link below to a page describing the performance results of database queries within a hierarchical object model, where search conditions are used at various levels of the hierarchy. Performance was evaluated across three different database sizes, with four variations in indexing strategies used for each.
- Performance Benchmarking on
Many-to-Many (M:N) Relationships with Variations in Indexing and Sizes of Object Databases
Performance Comparison with Multiple Query Conditions in an Object Hierarchy
The same object model and its twelve databases also provide an excellent platform for performance tests of a new category of RQL database searches, where data structures are automatically resolved for search result objects.
For convenience, and as a quick refresher, the 12 Java classes of the object model are presented below, both in a text box and illustrated in the accompanying image.
The object model consists of 12 Java classes N1-N4, M1-M4 and S1-S4.
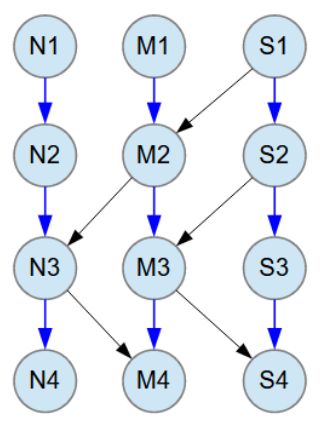
Blue arrow relationships between classes are M:N (many-to-many). All M:N relationships have 1-3 child objects at random.
Black arrow relationships between classes are M:1 (many-to-one).
The twelve object databases for testing are categorized into three groups based on size, with object counts of 12 x 100K, 12 x 1M, and 12 x 2M (where K = Thousand, M = Million), as shown in the table below. Each group is tested using four indexing strategies: no indexing (none), indexing only the value fields (value fields), indexing only the relationships (all relations), and the most comprehensive strategy, indexing both value fields and all relationships (value fields, all relations).
Please note that the table below is identical to the one shown on the page Performance Benchmarking on Many-to-Many (M:N) Relationships with Variations in Indexing and Sizes of Object Databases at the link table. These exact same databases are used in the tests on this page to produce identical search results, ensuring that the search results from these two different benchmark pages are fully comparable.
| RootDB Object Databases on MariaDB | |||||
|---|---|---|---|---|---|
| Database Name | Number of Objects | Indexes | Creation Time (s) | Objects per Second | Database Size (GB) |
| ex100Knx | 12 x 100K | none | 87 | 13764 | 0,644 |
| ex100Kvx | 12 x 100K | value fields | 93 | 12940 | |
| ex100Krx | 12 x 100K | all relations | 1532 | 783 | |
| ex100Kvrx | 12 x 100K | value fields, all relations | 1614 | 744 | 0,872 |
| ex1Mnx | 12 x 1M | none | 856 | 14022 | 5,18 |
| ex1Mvx | 12 x 1M | value fields | 1016 | 11809 | |
| ex1Mrx | 12 x 1M | all relations | 16238 | 739 | |
| ex1Mvrx | 12 x 1M | value fields, all relations | 16304 | 736 | 7,06 |
| ex2Mnx | 12 x 2M | none | 1641 | 14622 | 10,3 |
| ex2Mvx | 12 x 2M | value fields | 2161 | 11101 | |
| ex2Mrx | 12 x 2M | all relations | 31889 | 753 | |
| ex2Mvrx | 12 x 2M | value fields, all relations | 32605 | 736 | 13,6 |
Processor = AMD Ryzen 7 3700X, Disk Samsung SSD 860 EVO M.2 1TB
These 12 object databases offer a comprehensive platform for testing database queries using the 12 Java class object model described above. The following sections provide a detailed description and discussion of the new category of RQL queries and their tests conducted with these 12 databases.
New Category of RQL Queries with Variations in Indexing and Object Database Sizes
12 Object Databases Tested in MariaDB
The search conditions for performance testing of the object databases listed above are illustrated in the image below. Red X marks indicate the classes N3, M4, and S4, where search conditions are applied to their value fields. The first query used to evaluate performance returns objects from classes M1 and S1 as complete data structures, including all objects reachable from the root classes, marked with blue Xs. The paths from these root classes to the search condition classes are highlighted with red dashed lines.
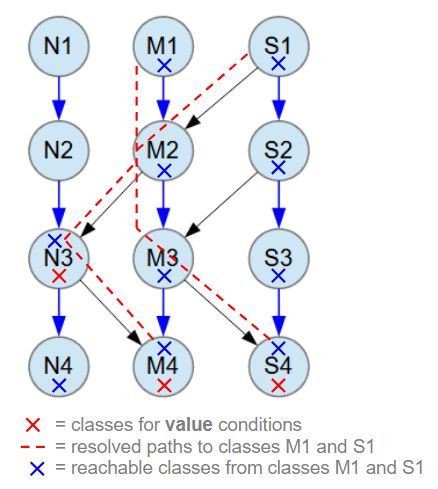
Blue arrow relationships between classes are M:N (many-to-many). All M:N relationships have 1-3 child objects at random.
Black arrow relationships between classes are M:1 (many-to-one).
The source code for the query is shown below, using three query variables: Q1, Q2, and Q4 to form the query expressions. Q1 merges the results of Q2 and Q4 to produce the final query result. The query is executed with query.queryQ1Objects(), initiating a complex set of operations. Both Q2 and Q4 have resolveObjectModel set to true, ensuring their root objects are automatically resolved. While M1 and S1 are the only possible root types for the final results, N1 objects can appear among the resolved N3 objects in Q2, as N3 is part of the N1 data structure. The merge operator in Q1 only accepts objects with the same root object instance from its operands, eliminating all possible N1 objects since Q4 cannot return them.
The RootStore variable r3 is used to query N3 objects from the object database, passed as the first parameter in the addQ2Query method, which creates the Q2 query variable. The Q2 search condition is defined for N3 objects as ((value=976), (m4.value=770)), where the first condition refers to N3's value field, and the second to m4.value, which accesses the value field in the referenced M4 object. In OOP, dot notation is commonly used to access fields in data structures. Here, lowercase names like m4 indicate a reference field to class M4, which is otherwise the same but written with a capital letter. This notation applies to all reference fields in the object model for these tests.
The two search conditions in Q2 are separated by a comma, indicating that an object must satisfy both conditions in its data structure. In this context, the comma functions like an AND operator and is frequently used due to its convenience in expressions.
The other query variable Q4 has a simple search condition (value = 50) which is set to search only for objects of the S4 class. S4 objects belong to the data structures of classes M1 and S1, which are resolved because the resolveObjectModel attribute is set to true for Q4. Finally, the merge operator in Q1 combines objects from its operands Q2 and Q4 if their root objects are the same, with the merged object representing the union of their data structures.
Q1 has the query expression "(Q2 MERGE Q4)", which merges the results of Q2 and Q4 to produce the final query result. However, Q1 does not inherently use the automatic resolving method for the query variables Q2 and Q4 in its query expression. By default, RQL follows a basic object-oriented programming (OOP) approach, where query variables (Q2 and Q4) are executed, and their results are merged without any root object resolving.
To enable automatic resolving of objects, the resolveObjectModel attribute must be set to true for Q1 by calling the method setQ1ResolveObjectModel(true). While M1 and S1 are the only possible root types for the final results, N1 objects may still appear among the resolved N3 objects in Q2, as N3 is part of the N1 data structure. The MERGE operator only accepts objects with the same root object instance from its operands, effectively excluding all N1 objects since Q4 cannot return them.
All of the above is executed when the query.queryQ1Objects() method is called.
RQL query:
RootStore r3 = rdb.getRootStore("fi.rootrql.example9wrx.N3"); // N3
RootStore r12 = rdb.getRootStore("fi.rootrql.example9wrx.S4"); // S4
Query query = Query.createQuery()
.addQ1Query(r3, "(Q2 MERGE Q4)")
.setQ1ResolveObjectModel(true)
.addQ2Query(r3,"(value = 976, m4.value = 770)")
.setQ2ResolveObjectModel(true)
.addQ4Query(r12,"(value = 50)")
.setQ4ResolveObjectModel(true);
query.queryQ1Objects();
List<M1> listM1 = r3.transferObjectList("fi.rootrql.example9wrx.M1");
List<S1> listS1 = r3.transferObjectList("fi.rootrql.example9wrx.S1");
System.out.println("listM1 count=" + listM1.size());
System.out.println("listS1 count=" + listS1.size());
The actual results of the database search are objects from the M1 and S1 classes, which must be retrieved separately from the r3 RootStore object using its transferObjectList method, as shown in the source code above. The retrieved objects are specified by the canonical name of the class, passed as a parameter in the transferObjectList method call.
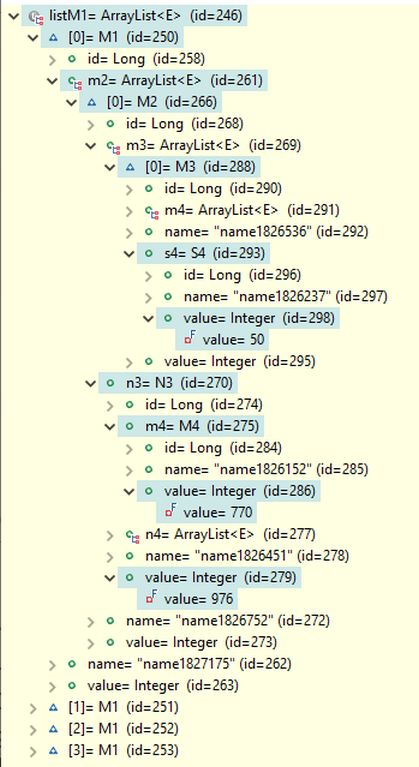
The results include complete data structures for M1 and S1 objects, which are resolved from the database search results. Examples of these structures are shown in the image below. For the first objects in the retrieved object lists, the paths through objects and fields leading to the fields used in the search conditions are highlighted. Since the data structures for M1 and S1 objects are complete, they also include objects that do not meet the search conditions.
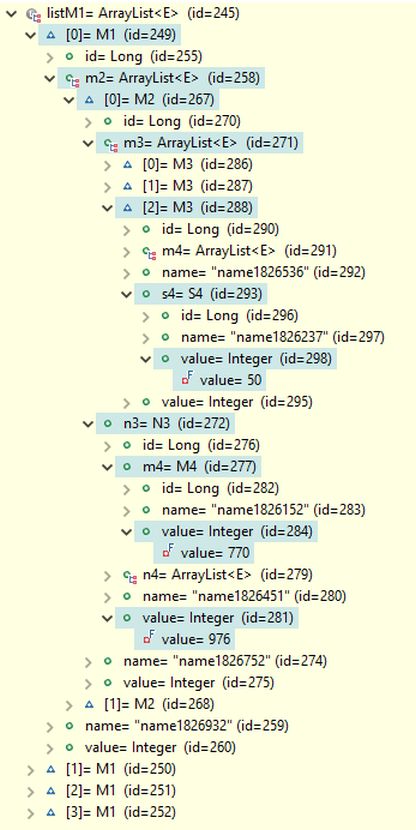
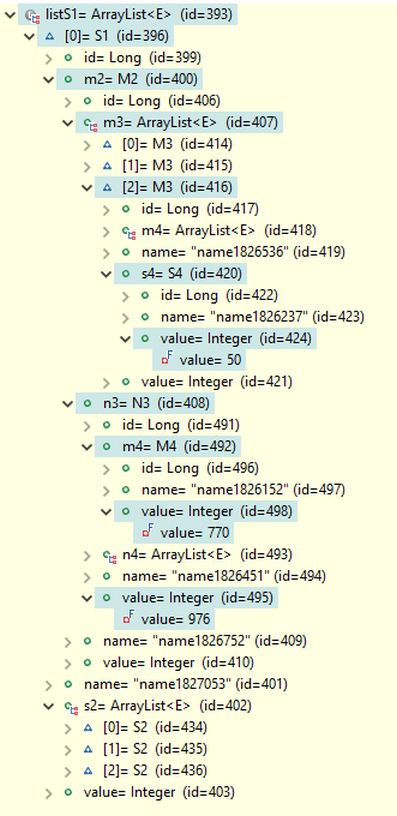
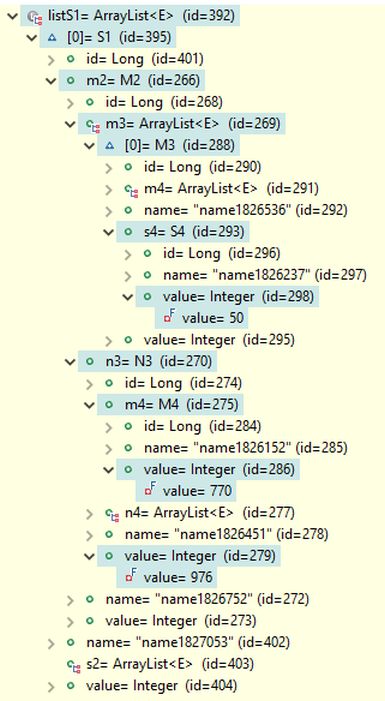
As an alternative, RQL provides the parts attribute, which can be set to true by calling query.setParts(true) when only the portions of the data structures used to fulfill the search conditions should be included in the results. The results with the parts attribute set to true are shown in the image below. Now, only objects on the paths through objects and fields leading to the fields used in the search conditions are included and visible in the debug views of the object lists presented below. The results are more concise, and in fact, complete data structures are often unnecessary. For this reason, RQL also provides convenient methods to precisely define which parts of the data structures should be included in the results. However, these methods are not covered here.
Note that, in principle, the results could have also included S1 objects with paths S1-S2-S3-S4 and S1-S2-M3-S4, but no such objects existed that fulfilled all the search conditions along with the MERGE operator union on the Q2 results. The only S1 object found has the path S1-M2-M3-S4 to the searched object S4.
Based on the object model, it is also known that S4 objects are not part of the data structure of class N1, meaning there is no path from N1 to S4. For this reason, N1 objects cannot appear in the database search results either.
The twelve object databases with variations in indexing and object counts were all tested using the same query described above. The results categorized by database size and indexing strategy are presented in the table below.
| RootDB Object Databases on MariaDB | Execution Times / Seconds | ||||||
|---|---|---|---|---|---|---|---|
| Database Name | Number of Objects | Indexes | Found M1 Objects | Found S1 Objects | Total | Create Objects | Search |
| ex100Knx | 12 x 100K | none | 4 | 1 | 7,867 | 0,029 | 7,838 |
| ex100Kvx | 12 x 100K | value fields | 4 | 1 | 5,787 | 0,028 | 5,759 |
| ex100Krx | 12 x 100K | all relations | 4 | 1 | 1,706 | 0,030 | 1,676 |
| ex100Kvrx | 12 x 100K | value fields, all relations | 4 | 1 | 0,635 | 0,037 | 0,598 |
| ex1Mnx | 12 x 1M | none | 40 | 10 | 97,758 | 0,296 | 97,46 |
| ex1Mvx | 12 x 1M | value fields | 40 | 10 | 59,531 | 0,273 | 59,26 |
| ex1Mrx | 12 x 1M | all relations | 40 | 10 | 25,213 | 0,234 | 24,98 |
| ex1Mvrx | 12 x 1M | value fields, all relations | 40 | 10 | 5,371 | 0,215 | 5,16 |
| ex2Mnx | 12 x 2M | none | 80 | 20 | 219,410 | 0,515 | 218,90 |
| ex2Mvx | 12 x 2M | value fields | 80 | 20 | 126,063 | 0,558 | 125,50 |
| ex2Mrx | 12 x 2M | all relations | 80 | 20 | 51,473 | 0,483 | 50,99 |
| ex2Mvrx | 12 x 2M | value fields, all relations | 80 | 20 | 19,234 | 0,453 | 18,78 |
Processor = AMD Ryzen 7 3700X, Disk Samsung SSD 860 EVO M.2 1TB
The test results of the query expression (m2.n3.value = 976, m2.m3.s4.value = 50, m2.n3.m4.value = 770) in Performance Benchmarking on Many-to-Many (M:N) Relationships can serve as a reference for comparing the results presented above. While the query results are essentially the same, the approach to retrieving the data structures differs significantly. The results are identical for M1 class objects, but the referenced test does not search for S1 class objects in the results. This makes it slightly more efficient in principle, but the way root objects are resolved has a much greater impact on execution time.
In the referenced test, the exact paths from root classes to the searched objects are specified in the search condition. Here, the search conditions are placed within the data structure, explicitly including only the parts where the field value conditions are set in the query expressions. This requires the database system to resolve the routes to the root classes based on the object model, making it a much more complex task.
The comparison of execution times for these two tests is expressed as a coefficient, indicating how many times this test is slower than the reference test. The results are presented below for each indexing strategy.
-
No Indexing: 1,5 - 1,9 x slower.
-
Value Fields Indexing: 1,7 - 1,9 x slower.
-
All Relations Indexing: 1,0 - 1,9 x slower.
-
Value Fields and All Relations Indexing: 1,1 - 1,7 x slower.
As expected, automatic resolving of root objects results in noticeably longer execution times. However, the performance remains reasonably good, as the times are still less than twice as long as the excellent reference times.
Enhancing Efficiency by Limiting Classes in Resolving Roots
RQL provides a significant improvement to database searches by appending a list of object model classes permitted for use in each search condition. The list is assigned to query variables Qn by invoking the setResolveRoots method, passing a parameter that contains a list of allowed class canonical names. The order of the classes in the list does not matter.
To visualize and help in understanding the use of the setResolveRoots method, the object model image with the expected search result paths is repeated below.

Blue arrow relationships between classes are M:N (many-to-many). All M:N relationships have 1-3 child objects at random.
Black arrow relationships between classes are M:1 (many-to-one).
In the source code below, the previously tested database search without the setResolveRoots method is rewritten using it to limit the allowed scope of classes in resolving root objects. Both query variables Q2 and Q4 are appended with the relevant canonical class names for the database search, ensuring they include all the classes required along the result paths to the root classes M1 and S1. However, classes S3 and S2 are excluded because the path through them is not intended to be part of the results. Additionally, classes N2 and N1 were excluded because it is known from the object model that S4 objects are not part of the data structure of class N1, meaning there is no path from N1 to S4.
RQL query:
RootStore r3 = rdb.getRootStore("fi.rootrql.example9wrx.N3"); // N3
RootStore r12 = rdb.getRootStore("fi.rootrql.example9wrx.S4"); // S4
Query query = Query.createQuery()
.addQ1Query(r3, "(Q2 MERGE Q4)")
.setQ1ResolveObjectModel(true)
.addQ2Query(r3,"(value = 976, m4.value = 770)")
.setQ2ResolveRoots(
"fi.rootrql.example9wrx.M2",
"fi.rootrql.example9wrx.M1",
"fi.rootrql.example9wrx.S1")
.addQ4Query(r12,"(value = 50)")
.setQ4ResolveRoots(
"fi.rootrql.example9wrx.M3",
"fi.rootrql.example9wrx.M2",
"fi.rootrql.example9wrx.M1",
"fi.rootrql.example9wrx.S1");
query.queryQ1Objects();
List<M1> listM1 = r3.transferObjectList("fi.rootrql.example9wrx.M1");
List<S1> listS1 = r3.transferObjectList("fi.rootrql.example9wrx.S1");
System.out.println("listM1 count=" + listM1.size());
System.out.println("listS1 count=" + listS1.size());
The twelve object databases, varying in indexing and object counts, were all tested using the same query described in the source code above. The results categorized by database size and indexing strategy are presented in the table below.
| RootDB Object Databases in MariaDB | Execution Times / Seconds | ||||||
|---|---|---|---|---|---|---|---|
| Database Name | Number of Objects | Indexes | Found M1 Objects | Found S1 Objects | Total | Create Objects | Search |
| ex100Knx | 12 x 100K | none | 4 | 1 | 5,022 | 0,030 | 4,992 |
| ex100Kvx | 12 x 100K | value fields | 4 | 1 | 3,440 | 0,031 | 3,409 |
| ex100Krx | 12 x 100K | all relations | 4 | 1 | 1,639 | 0,032 | 1,607 |
| ex100Kvrx | 12 x 100K | value fields, all relations | 4 | 1 | 0,386 | 0,053 | 0,333 |
| ex1Mnx | 12 x 1M | none | 40 | 10 | 52,472 | 0,254 | 52,218 |
| ex1Mvx | 12 x 1M | value fields | 40 | 10 | 37,702 | 0,279 | 37,422 |
| ex1Mrx | 12 x 1M | all relations | 40 | 10 | 12,158 | 0,228 | 11,930 |
| ex1Mvrx | 12 x 1M | value fields, all relations | 40 | 10 | 2,741 | 0,205 | 2,536 |
| ex2Mnx | 12 x 2M | none | 80 | 20 | 144,116 | 0,509 | 143,607 |
| ex2Mvx | 12 x 2M | value fields | 80 | 20 | 68,888 | 0,502 | 68,386 |
| ex2Mrx | 12 x 2M | all relations | 80 | 20 | 31,850 | 0,573 | 31,277 |
| ex2Mvrx | 12 x 2M | value fields, all relations | 80 | 20 | 10,675 | 0,493 | 10,182 |
The test results of the query expression (m2.n3.value = 976, m2.m3.s4.value = 50, m2.n3.m4.value = 770) from the Performance Benchmarking on Many-to-Many (M:N) Relationships are again used as a reference for comparing the results presented in the table above. While the query results are essentially the same, the approach to retrieving the data structures differs significantly. The results are identical for M1 class objects. As already noted, the referenced test does not search for S1 class objects, making it slightly more efficient in principle. However, in this case, the setResolveRoots method significantly improves root object searching by ensuring that irrelevant parts of the object model are not used unnecessarily.
The comparison of execution times between these two tests is expressed as a coefficient, indicating how many times this test is slower or faster than the reference test. A coefficient value greater than zero indicates a slower performance, while a value less than zero indicates a faster performance. The coefficient results are presented below for each indexing strategy.
-
No Indexing: 0,97 – 1,02
-
Value Fields Indexing: 0,90 – 1,17
-
All Relations Indexing: 0,92 – 1,4
-
Value Fields and All Relations Indexing: 0,53 – 0,92
As anticipated above, the obtained coefficients show that the database query performance is now much improved, either just as good or even slightly better than in the compared reference databases. The best improvement is achieved with indexing strategy Value Fields and All Relations Indexing, which has a coefficient of 0,53 for the database with a size of 12 x 1M. In fact, the largest databases, with sizes of 12 x 2M, have coefficients between 0,84 and 1,14, which is noteworthy because performance is especially crucial with larger databases. It is interesting to compare this to the first test, where the database size 12 x 2M has coefficients between 1,48 and 1,85, which is about 0,7 coefficient units worse. This indicates that resolving unnecessary parts of the object model, such as the data structure of the N1 class, resulted in this amount of performance loss.
Limiting the Resolving of Root Objects to M1 Objects
The allowed scope of classes in resolving root objects can be limited to include only the M1 class and classes in its associated data structure. This completes the performance comparison with the reference databases at link Performance Benchmarking on Many-to-Many (M:N) Relationships, as the database search results now consist of the exact same M1 objects.
The object model is visualized again in the image below, showing the searched objects marked with red Xs and the reachable classes from M1 marked with blue Xs that will be included in the database search results. The paths from the searched classes to the root class M1 are indicated by red dashed lines, used to limit the database search and make it as efficient as possible.
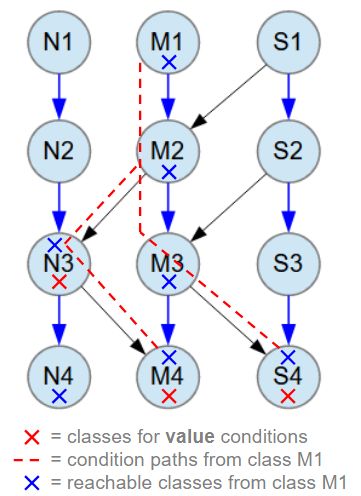
Blue arrow relationships between classes are M:N (many-to-many). All M:N relationships have 1-3 child objects at random.
Black arrow relationships between classes are M:1 (many-to-one).
In the source code below, the database searches for query variables Q2 and Q4 are limited to paths leading to the M1 class, as indicated by the red dashed lines shown above. The allowed classes are M1 and M2 for Q2, and M1, M2 and M3 for Q4, which are passed as parameters in their respective calls to the setResolveRoots method. The database search results are retrieved by calling the transferObjectList method only once, with the canonical name of the M1 class as the parameter, since the results cannot include any other objects.
RQL query:
RootStore r3 = rdb.getRootStore("fi.rootrql.example9wrx.N3"); // N3
RootStore r12 = rdb.getRootStore("fi.rootrql.example9wrx.S4"); // S4
Query query = Query.createQuery()
.addQ1Query(r3, "(Q2 MERGE Q4)")
.setQ1ResolveObjectModel(true)
.addQ2Query(r3,"(value = 976, m4.value = 770)")
.setQ2ResolveRoots(
"fi.rootrql.example9wrx.M2",
"fi.rootrql.example9wrx.M1")
.addQ4Query(r12,"(value = 50)")
.setQ4ResolveRoots(
"fi.rootrql.example9wrx.M3",
"fi.rootrql.example9wrx.M2",
"fi.rootrql.example9wrx.M1");
query.queryQ1Objects();
List<M1> listM1 = r3.transferObjectList("fi.rootrql.example9wrx.M1");
System.out.println("listM1 count=" + listM1.size());
The twelve object databases, varying in indexing and object counts, were all tested using the same query described in the source code above. The results categorized by database size and indexing strategy are presented in the table below.
| RootDB Object Databases in MariaDB | Execution Times / Seconds | ||||||
|---|---|---|---|---|---|---|---|
| Database Name | Number of Objects | Indexes | Found M1 Objects | Total | Create Objects | Search | |
| ex100Knx | 12 x 100K | none | 4 | 4,218 | 0,019 | 4,199 | |
| ex100Kvx | 12 x 100K | value fields | 4 | 2,677 | 0,021 | 2,656 | |
| ex100Krx | 12 x 100K | all relations | 4 | 1,587 | 0,018 | 1,569 | |
| ex100Kvrx | 12 x 100K | value fields, all relations | 4 | 0,276 | 0,032 | 0,244 | |
| ex1Mnx | 12 x 1M | none | 40 | 30,056 | 0,153 | 29,903 | |
| ex1Mvx | 12 x 1M | value fields | 40 | 26,548 | 0,161 | 26,387 | |
| ex1Mrx | 12 x 1M | all relations | 40 | 11,222 | 0,145 | 11,077 | |
| ex1Mvrx | 12 x 1M | value fields, all relations | 40 | 2,197 | 0,142 | 2,054 | |
| ex2Mnx | 12 x 2M | none | 80 | 113,089 | 0,313 | 112,776 | |
| ex2Mvx | 12 x 2M | value fields | 80 | 54,697 | 0,347 | 54,351 | |
| ex2Mrx | 12 x 2M | all relations | 80 | 29,412 | 0,298 | 29,114 | |
| ex2Mvrx | 12 x 2M | value fields, all relations | 80 | 8,632 | 0,316 | 8,316 | |
The test results of the query expression (m2.n3.value = 976, m2.m3.s4.value = 50, m2.n3.m4.value = 770) from the Performance Benchmarking on Many-to-Many (M:N) Relationships are again used as a reference for comparing the results presented in the table above. Now, the result of the database search for M1 objects is identical to the M1 objects returned by the reference database, although the approach to searching for objects is significantly different.
The comparison of execution times between these two tests is expressed as a coefficient, indicating how many times this test is slower or faster than the reference test. A coefficient value greater than zero indicates a slower performance, while a value less than zero indicates a faster performance. The coefficient results are presented below for each indexing strategy.
-
No Indexing: 0,58 – 0,84
-
Value Fields Indexing: 0,72 – 0,83
-
All Relations Indexing: 0,86 – 1,06
-
Value Fields and All Relations Indexing: 0,42 – 0,68
The database query performance is now significantly improved compared to the previous test case where S1 objects were also retrieved. In fact, with only one exception, the results are significantly better than the reference database, which can be considered a remarkable achievement for this new category of database searching. The exception is with the All Relations Indexing strategy on the largest database size, 12 x 2M, where the execution time is 1.06 times that of the reference database. While the difference is significant, it is not considerably worse. It is important to highlight that otherwise the largest databases with sizes of 12 x 2M have excellent coefficients ranging from 0.69 to 0.76. In practice, the larger the databases, the greater the importance of performance, and in this case (aside from one exception), the coefficients are excellent for the tested largest databases.
Limiting the Resolving of Root Objects to M2 Objects
As an example outside the primary scope of the actual benchmarking, which is the main focus of this page, the method setResolveRoots and its versatile ability to define the resolved classes is further demonstrated. In fact, it is not required that the specified classes lead to a class or classes at the boundary of the data structure. The resolving process can terminate at any class within the data structure.
For example, the method setResolveRoots can be used to terminate the resolving process at M2 objects instead of M1 objects. This is illustrated in the image below, showing the searched objects marked with red Xs and the reachable classes from M2 marked with blue Xs that will be included in the database search results. The paths from the searched classes to the root class M2 are indicated by red dashed lines, used to limit the database search and make it as efficient as possible.
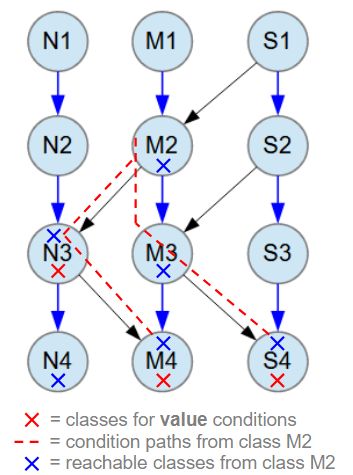
Blue arrow relationships between classes are M:N (many-to-many). All M:N relationships have 1-3 child objects at random.
Black arrow relationships between classes are M:1 (many-to-one).
In the source code below, the database searches for query variables Q2 and Q4 are limited to paths leading to the M2 class, as indicated by the red dashed lines shown above. The allowed classes are M2 for Q2, and M2 and M3 for Q4, which are passed as parameters in their respective calls to the setResolveRoots method. The database search results are retrieved by calling the transferObjectList method only once, with the canonical name of the M2 class as the parameter, since the results cannot include any other objects.
RQL query:
RootStore r3 = rdb.getRootStore("fi.rootrql.example9wrx.N3"); // N3
RootStore r12 = rdb.getRootStore("fi.rootrql.example9wrx.S4"); // S4
Query query = Query.createQuery()
.addQ1Query(r3, "(Q2 MERGE Q4)")
.setQ1ResolveObjectModel(true)
.addQ2Query(r3,"(value = 976, m4.value = 770)")
.setQ2ResolveRoots(
"fi.rootrql.example9wrx.M2")
.addQ4Query(r12,"(value = 50)")
.setQ4ResolveRoots(
"fi.rootrql.example9wrx.M3",
"fi.rootrql.example9wrx.M2");
query.queryQ1Objects();
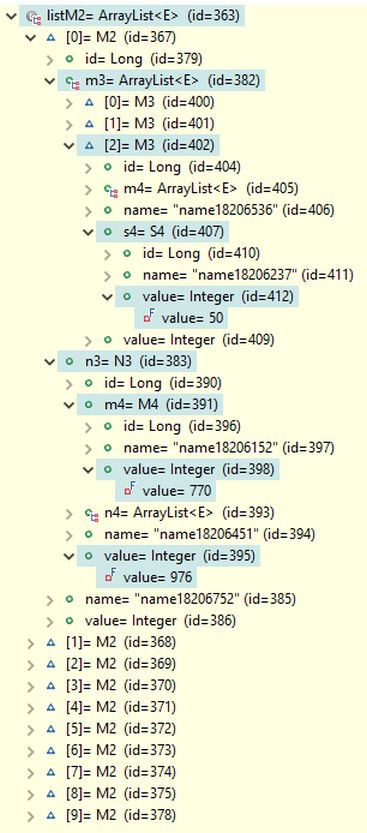
List<M2> listM2 = r3.transferObjectList("fi.rootrql.example9wrx.M2");
System.out.println("listM2 count=" + listM2.size());
In the debug view below, the 10 found objects of the M2 class are displayed, with the first object expanded to the fields where the search conditions were set. Notice that the parts attribute has a value of false (as its default value is false), meaning that complete objects are returned, not just the parts of M2 objects where the search conditions are applied.
Summary
The strength of this new category of database searches lies in the flexibility to set multiple search conditions anywhere within the data structures of objects without defining the root objects of the possible or expected query result objects. This complex query is automatically and efficiently resolved, even though it involves finding root objects from multiple different classes along with their associated data structures.
Three slightly different approaches to using the same database searches have been presented above, providing a representative view of the versatility and flexibility offered by the RQL search language.
The performance is compared to the corresponding results on page Performance Benchmarking on Many-to-Many (M:N) Relationships with Variations in Indexing and Sizes of Object Databases, see link Performance Comparison with Multiple Query Conditions in an Object Hierarchy. It used the RQL query expression (m2.n3.value = 976, m2.m3.s4.value = 50, m2.n3.m4.value = 770), where all the search conditions start from the root class M1, which is also the type of the query result objects. This approach to defining search conditions completely avoids the problem of determining the possible type or types of root objects, as it is already specified within the query expression itself. It can also be assumed that this is the most efficient way to perform such a database search, as the search criteria can be executed in a straightforward manner without needing to explore other possible routes to root objects within the object model. For this reason, the performance tests conducted above, based on the new category of database searches, use this database search and its performance results with the 12 databases as a comparison reference.
The First Test: No Guidance in Resolving Root Objects
In the first tested database search, the search conditions are set for classes N3 and S4 in query variables Q2 and Q4, respectively, with the resolveObjectModel attribute set to true for both. In practice, setting the attribute to true specifies that the query variables request automatic resolving of root classes from the object model during the search for the actual root objects. This means that all classes that include N3 or S4 in their data structure must be considered in the search and determination of root classes. As a result, class N1 is also included among the possible root classes, which leads to searching for N2 and N1 objects for the objects found in query variable Q2. This is done even though it is self-evident that the final result cannot contain any N1 objects, as its data structure does not include class S4. In other words, according to the object model, S4 objects cannot be reached from N1 objects.
The results are the complete data structures of M1 and S1 objects, which are resolved for the database search results found for the search conditions set to N3 and S4. It is noteworthy that the results include root objects from two distinct classes M1 and S1. In other words, this type of query can return objects from multiple different root classes. The performance test results clearly show the overhead caused by the additional work of fully resolving the object model and performing unnecessary searches, such as for objects of the root class N1. Part of the difference is due to the fact that the tests with the reference databases retrieve only M1 root objects, not S1, though the exact impact on execution time is difficult to estimate. The retrieved M1 objects are exactly the same as in the test here. On these considerations, the performance is reasonably good because the execution times are less than twice as long as the excellent reference times from the tests with the reference databases. Leaving all the analysis of the object model to the automatic resolving mechanism is certainly the most carefree and convenient way to write database searches, as the search conditions can simply be placed in different places of the data structures, and the database search system handles everything else. In fact, this provides a unique and previously unseen way to perform database searches on networks of objects that form complex data structures.
The Second Test: Enhancing Efficiency by Limiting Classes in Resolving Roots
In the second tested database search, the search conditions are also set for classes N3 and S4 in query variables Q2 and Q4, respectively. However, instead of using the resolveObjectModel attribute, the setResolveRoots attribute is used with a list of class canonical names passed as its parameter. The canonical names are intended to cover all classes along the routes to the expected query result root classes, and the canonical names are used to limit the resolving of objects to only those classes in the object model. The canonical name classes are also highlighted with red dashed lines in the image illustrating this test above.
The results are the exact same complete data structures of M1 and S1 objects as in the first test, but the performance should now be improved due to the use of setResolveRoots attributes for query variables Q2 and Q4. In fact, the performance is significantly improved. For example, the biggest database size 12 x 2M shows execution times that are approximately 60 percent of the times recorded in the first test. Execution times are either about equal to or even slightly better than those in the reference databases used for comparison.
This is somewhat suspicious or concerning, as the tests with the reference database use a highly efficient definition of search criteria, where the dot notation precisely describes the path through the object fields to the searched objects.
However, it is known that the database search algorithm used here is highly suitable for parallel computing with multiple threads. This is likely why the field name sequences used in the reference database turn out to be at least slightly less efficient in this regard. This presents a clear target for further development, as it would be natural to expect that a more deterministic search should also result in better performance.
The second test demonstrated that database searches can be made significantly more efficient when the search conditions are supplemented with a list of canonical class names from the object model that are necessary for query execution.
The Third Test: Limiting the Resolving of Root Objects to M1 Objects
In the third tested database search, the search conditions are once again set for classes N3 and S4 in query variables Q2 and Q4, respectively. However, the list of class canonical names set in the setResolveRoots attribute is now restricted to classes needed to resolve only the root objects of the M1 class and their data structures. As a result, root objects of the S1 class and their data structures are excluded from the search, which should further enhance query performance. The included canonical name classes are also highlighted with red dashed lines in the image illustrating this test above. The third test is particularly interesting because, for the first time, the results are completely identical to those of the reference database, making them fully comparable.
The performance results are significantly better than the reference database, which can be considered a remarkable achievement for this new category of database searching. For example, with the indexing strategy value fields and all relations, the database sizes 12 x 100K, 12 x 1M, and 12 x 2M show execution times that are approximately 70, 42, and 70 percent, respectively, of the times recorded in the same tests on the reference database. The independence of performance from the size of the database reinforces the belief that this new category of database queries is already highly significant and holds great potential as a future alternative in database development.
Conclusions
The object model used in the performance tests on this page, which has also been used in other tests on this site, has proven to be sufficiently complex in its data structure, making it suitable for researching object writing speeds and comparing different database querying strategies across three database sizes (12 x 100K, 12 x 1M, and 12 x 2M objects) using four indexing strategies: no indexing (none), indexing only the value fields (value fields), indexing only the relationships (all relations), and the most comprehensive strategy, indexing both value fields and all relationships (value fields, all relations).
An object model like the one used here provides a solid foundation for creating arbitrarily large yet well-defined object models for demanding database tests. It consists of a number of objects arranged in a grid-like network, which can be easily scaled up by increasing the number of objects in both the width and height directions. In addition, the quantity and quality of relationships between objects, along with the database size and indexing strategies, can be easily adjusted to meet the specific objectives and goals of the tests.
In this new category of database queries, search conditions are placed within the data structure. The query expressions contain only the specific parts of the object model where the search conditions apply. Often, the root classes that the query is expected to return are not included in the query expression at all. This requires the database system to automatically determine the paths to the root classes based on the object model. The process is highly complex, as at each step, the system must identify the relevant classes and their objects in the database. Based on the objects found, if any, this process continues until the root objects are identified. The complexity increases further when the object model includes recursion, which can introduce cycles, or inheritance. However, both recursion and inheritance are fully supported and allowed.
As demonstrated by the results, despite its complexity, the implementation performs surprisingly well. The execution times are still less than twice as long as the excellent execution times of the reference database, which uses query expressions that explicitly define the paths from the expected root class to the classes where the value conditions are applied.
It is also demonstrated that in RQL, the method setResolveRoots can be used to specify a list of canonical class names, limiting the resolving process to only those classes within the object model. This has a highly positive impact on performance, as fewer classes are involved in the resolving process. In fact, when the classes were restricted to exactly those returned by the reference database, the execution times were significantly shorter than those of the reference database. This provides remarkable evidence that the process and its algorithm have been successfully implemented and can be considered exceptionally efficient.
In the tests presented here, performance is evaluated from two key perspectives: the speed of writing objects to the database and the efficiency of searching for objects with conditions that span multiple classes within the object model hierarchy.
Evaluating Object Writing Speed
The test results show that the speed of writing objects to the database varies significantly depending on the applied indexing strategy. The fastest writing speed is achieved without any indexing and is approximately 20 times faster than the slowest, which uses the indexing strategy that covers both value fields and all relationships (value fields, all relations) When indexing is applied to value fields only, the speed is still 15 times faster than the slowest, which is also a notably good result. Another aspect related to writing speed is its behavior as the database size increases with the growing number of objects. However, all three databases with different sizes (12 x 100K, 12 x 1M, and 12 x 2M) operated at approximately the same writing speed when compared to each other using the same indexing strategies. The writing speed is excellent without indexing or when indexing only value fields. In other cases, it remains acceptable, as more comprehensive indexing always reduces writing speed. This is the trade-off for achieving better or even excellent query performance. Based on the measured variations of writing speed in the test results, it is important to evaluate writing speed with all possible and reasonable indexing strategies, as these results help identify and select the most suitable and sufficiently efficient indexing for each use case.
The conclusions about object writing speed are outlined in the following two points.
-
The object writing speed is excellent (more than 10,000 objects per second) across all tested database sizes when using either no indexing (none) or only value fields are indexed. However, performance may deteriorate if many fields per object class need to be indexed (this was not specifically tested here).
-
The object writing speed is good (more than 700 objects per second) across all tested database sizes when indexing either all relationships (all relations) or both value fields and relationships (value fields, all relations).
Evaluating the Efficiency of Object Queries
Contrary to writing speed, query performance benefits from the use of indexes in a database, as the primary purpose of indexing is to improve performance. However, it is not always clear how much indexing or what indexing strategy is actually needed for different database sizes and structures. If the database query use cases are known in advance, indexing can be tailored precisely for them. Otherwise, a more general plan can be applied to ensure reasonable query times. While the initial indexing strategy can be modified at any time, doing so always involves additional work.
In relational databases, it's not uncommon to index as many columns as possible due to concerns that queries may become slow, very slow, or even stuck, especially when joins are involved. Similarly, queries in RootDB/RQL object databases also benefit from indexing fields that are occasionally or rarely used. However, the key difference in RootDB/RQL databases is that query slowdowns are typically very moderate and never result in the query becoming completely stuck. This approach provides an alternative where the focus shifts toward optimizing the speed of writing objects to the database, rather than maximizing query performance. Such an approach is feasible because database searches remain sufficiently fast even with a less comprehensive indexing strategy.
The conclusions about database search performance in relation to the applied indexing strategies are presented in the following three points.
-
Small databases (12 x 100K) may not require indexing at all (none). If a query time faster than 4 seconds is needed, indexing the value fields used in queries is preferable, as the writing speed of objects remains nearly as fast as without indexing. However, performance may deteriorate if many fields per object class need to be indexed (this was not specifically tested here).
-
Indexing all relations reduces query time by roughly half compared to indexing value fields, which offers a much better writing speed, nearly the same as without indexing (none). However, indexing all relations alone might be a good choice due to its approximately double search performance. The benefit of indexing all relations instead of value fields will likely increase if the number of value fields grows (the tests here included only one value field per class). Notably, even in the case of relational databases, documentation about their database queries very rarely, if ever, presents the option of indexing only the relationships.
-
When the best possible performance is required for database queries, at a minimum, all value fields and relationships (value fields, all relations) used in the search conditions must be indexed. The database size increases by approximately 30 percent compared to the case without indexing (none), but storage space is not a significant issue nowadays. The writing time of objects to the database is about 20 times longer than without indexing, but this is acceptable when maximum query performance is a priority
Performance Outlook
The tests were conducted on five-year-old hardware (processor and SSD). Modern multi-core processors and SSDs could potentially deliver RootDB/RQL execution times more than ten times faster. Investing in up-to-date processors and memory is certainly worthwhile, especially in production environments. The performance improvements offered by modern hardware can be easily estimated by scaling the results from the above tests by a factor of 10, for example. These hypothetical, yet realistic, new test results of Limiting the Resolving of Root Objects to M1 Objects are presented in the table below.
| RootDB Object Databases in MariaDB | Execution Times / Seconds | ||||||
|---|---|---|---|---|---|---|---|
| Database Name | Number of Objects | Indexes | Found M1 Objects | Total | Create Objects | Search | |
| ex100Knx | 12 x 100K | none | 4 | 0,4218 | 0,0019 | 0,4199 | |
| ex100Kvx | 12 x 100K | value fields | 4 | 0,2677 | 0,0021 | 0,2656 | |
| ex100Krx | 12 x 100K | all relations | 4 | 0,1587 | 0,0018 | 0,1569 | |
| ex100Kvrx | 12 x 100K | value fields, all relations | 4 | 0,0276 | 0,0032 | 0,0244 | |
| ex1Mnx | 12 x 1M | none | 40 | 3,056 | 0,0153 | 2,9903 | |
| ex1Mvx | 12 x 1M | value fields | 40 | 2,6548 | 0,0161 | 2,6387 | |
| ex1Mrx | 12 x 1M | all relations | 40 | 1,1222 | 0,0145 | 1,1077 | |
| ex1Mvrx | 12 x 1M | value fields, all relations | 40 | 0,2197 | 0,0142 | 0,2054 | |
| ex2Mnx | 12 x 2M | none | 80 | 11,309 | 0,0313 | 11,278 | |
| ex2Mvx | 12 x 2M | value fields | 80 | 5,470 | 0,0347 | 5,435 | |
| ex2Mrx | 12 x 2M | all relations | 80 | 2,941 | 0,030 | 2,911 | |
| ex2Mvrx | 12 x 2M | value fields, all relations | 80 | 0,863 | 0,032 | 0,832 | |
The test results demonstrate excellent query times, well below one second across all database sizes when the most comprehensive indexing (value fields and all relations) is applied. Notably, even without indexing (none), the results are still quite promising, with query times of 0.42, 3 and 11 seconds for database sizes of 12 x 100K, 12 x 1M and 12 x 2M, respectively. By avoiding indexing, these times remain acceptable for many applications, while benefiting from an impressive write speed of nearly 15,000 objects per second and a reduced overall database size.
Performance Comparison to AMD Ryzen 9 9950X 16-Core Processor 4,3 GHz
To validate the above performance outlook, the performance test Limiting the Resolving of Root Objects to M1 Objects was conducted on a system equipped with an AMD Ryzen 9 9950X 16-Core Processor (4.3 GHz), effectively doubling the processor count compared to the original test environment. The results of these performance tests are summarized in the table below.
| RootDB Object Databases in MariaDB | Execution Times / Seconds | ||||||
|---|---|---|---|---|---|---|---|
| Database Name | Number of Objects | Indexes | Found M1 Objects | Total | Create Objects | Search | Search Improvement Coefficient |
| ex100Knx | 12 x 100K | none | 4 | 2,204 | 0,0231 | 2,181 | 2,18 |
| ex100Kvx | 12 x 100K | value fields | 4 | 1,414 | 0,0241 | 1,390 | 1,91 |
| ex100Krx | 12 x 100K | all relations | 4 | 0,911 | 0,0201 | 0,891 | 1,76 |
| ex100Kvrx | 12 x 100K | value fields, all relations | 4 | 0,198 | 0,0251 | 0,173 | 1,41 |
| ex1Mnx | 12 x 1M | none | 40 | 9,161 | 0,1703 | 8,991 | 3,33 |
| ex1Mvx | 12 x 1M | value fields | 40 | 9,062 | 0,1726 | 8,889 | 2,97 |
| ex1Mrx | 12 x 1M | all relations | 40 | 6,386 | 0,1745 | 6,211 | 1,78 |
| ex1Mvrx | 12 x 1M | value fields, all relations | 40 | 1,516 | 0,1736 | 1,342 | 1,53 |
| ex2Mnx | 12 x 2M | none | 80 | 32,639 | 0,3516 | 32,287 | 3,49 |
| ex2Mvx | 12 x 2M | value fields | 80 | 29,118 | 0,3666 | 28,751 | 1,89 |
| ex2Mrx | 12 x 2M | all relations | 80 | 13,302 | 0,3302 | 12,972 | 2,24 |
| ex2Mvrx | 12 x 2M | value fields, all relations | 80 | 2,933 | 0,3351 | 2,598 | 3,20 |
Processor = AMD Ryzen 9 9950X, Disk = Samsung SSD 990 PRO 2TB
The test results demonstrate query search time improvements ranging from 1.41x to 3.49x. Notably, 6 out of the 12 tests achieve more than a twofold improvement, surpassing the gains expected solely from the doubling of processor cores. Searches without indexing (none) achieve the best average improvement, with search time gains of 2.18x, 3.33x, and 3.49x for database sizes of 12 x 100K, 12 x 1M, and 12 x 2M, respectively. Additionally, databases without indexing benefit from a reduced overall size and achieve an impressive write speed of nearly 24,000 objects per second, effectively utilizing the enhanced processor capacity.
Based on these test results with the 16-core processor, it can be estimated that a computer with five times the core count - equivalent to 80 cores - could potentially reduce the original search times by a factor of ten, as outlined in the above performance outlook. For instance, the AMD EPYC 9684X, a processor with 96 cores, exceeds the required core count by a significant margin. However, its price of approximately $10,000 may still limit its adoption in database server deployments.
Links to other pages on this site.
- Performance Comparison Many-to-Many (M:N) Relationships with Indexing
- Performance Comparison Many-to-Many (M:N) Relationships without Indexing
- Performance Benchmarking on Many-to-Many (M:N) Relationships with Variations in Indexing and Sizes of Object Databases: Performance Comparison with Multiple Query Conditions in an Object Hierarchy
- RootDB, Technical Features
- RootDB and RQL, Home
Page content © 2025

Contact us:
